TRABAJO MECÁNICO.- WIKIPEDIA

Trabajo (física)

(Redirigido desde «Trabajo mecanico»)

Trabajo (W)
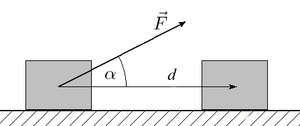Trabajo realizado por una fuerza constante.
Magnitud	Trabajo (W)
Definición	Producto de la fuerza ejercida sobre un cuerpo por su desplazamiento
Tipo	Magnitud escalar
Unidad SI	Julio (J)
Otras unidades	Kilojulio (kJ) Kilográmetro (kgm)
[editar datos en Wikidata]

En mecánica clásica, se dice que una fuerza realiza trabajo cuando altera el estado de movimiento de un cuerpo. El trabajo de la fuerza sobre ese cuerpo será equivalente a la energía necesaria para desplazarlo¹ de manera acelerada. El trabajo es una magnitud físicaescalar que se representa con la letra ${\displaystyle \ W}$ (del inglés Work) y se expresa en unidades de energía, esto es en julios o joules (J) en el Sistema Internacional de Unidades.

Ya que por definición el trabajo es un tránsito de energía,² nunca se refiere a él como incremento de trabajo, ni se simboliza como ΔW.

Índice

  [ocultar] 

• 1El trabajo en mecánica
  • 1.1Casos particulares
  • 1.2Trabajo y energía cinética
• 2El trabajo en termodinámica
• 3Unidades de trabajo
  • 3.1Sistema Internacional de Unidades
  • 3.2Sistema Técnico de Unidades
  • 3.3Sistema Cegesimal de Unidades
  • 3.4Sistema Anglosajón de Unidades
  • 3.5Sistema anglosajón
  • 3.6Otras unidades
• 4Véase también
• 5Referencias
  • 5.1Bibliografía
• 6Enlaces externos

El trabajo en mecánica[editar]

Trabajo de una fuerza.

Consideremos una partícula ${\displaystyle P}$ sobre la que actúa una fuerza ${\displaystyle F}$, función de la posición de la partícula en el espacio, esto es ${\displaystyle F=F(\mathbf {r} )}$ y sea ${\displaystyle \mathrm {d} \mathbf {r} }$ un desplazamiento elemental (infinitesimal) experimentado por la partícula durante un intervalo de tiempo ${\displaystyle \mathrm {d} t}$. Llamamos trabajo elemental, ${\displaystyle \mathrm {d} W}$, de la fuerza ${\displaystyle \mathbf {F} }$ durante el desplazamiento elemental ${\displaystyle \mathrm {d} \mathbf {r} }$ al producto escalar ${\displaystyle \ F\cdot \mathrm {d} \mathbf {r} }$; esto es,

${\displaystyle \mathrm {d} W=\mathbf {F} \cdot \mathrm {d} \mathbf {r} \,}$

Si representamos por ${\displaystyle \mathrm {d} s}$ la longitud de arco (medido sobre la trayectoria de la partícula) en el desplazamiento elemental, esto es ${\displaystyle \mathrm {d} s=|\mathrm {d} \mathbf {r} |}$ , entonces el vector tangente a la trayectoria viene dado por ${\displaystyle \mathbf {e} _{\text{t}}=\mathrm {d} \mathbf {r} /\mathrm {d} s}$ y podemos escribir la expresión anterior en la forma

${\displaystyle \mathrm {d} W=\mathbf {F} \cdot \mathrm {d} \mathbf {r} =\mathbf {F} \cdot \mathbf {e} _{\text{t}}\mathrm {d} s=(F\cos \theta )\mathrm {d} s=F_{\text{s}}\mathrm {d} s\,}$

donde ${\displaystyle \theta }$ representa el ángulo determinado por los vectores ${\displaystyle \mathrm {d} \mathbf {F} }$ y ${\displaystyle \mathbf {e} _{\text{t}}}$ y ${\displaystyle F_{\text{s}}}$ es la componente de la fuerza F en la dirección del desplazamiento elemental ${\displaystyle \mathrm {d} \mathbf {r} }$.

El trabajo realizado por la fuerza ${\displaystyle \mathbf {F} }$ durante un desplazamiento elemental de la partícula sobre la que está aplicada es una magnitud escalar, que podrá ser positiva, nula o negativa, según que el ángulo ${\displaystyle \theta }$ sea agudo, recto u obtuso.

Si la partícula P recorre una cierta trayectoria en el espacio, su desplazamiento total entre dos posiciones A y B puede considerarse como el resultado de sumar infinitos desplazamientos elementales ${\displaystyle \mathrm {d} \mathbf {r} }$ y el trabajo total realizado por la fuerza ${\displaystyle \mathbf {F} }$ en ese desplazamiento será la suma de todos esos trabajos elementales; o sea

${\displaystyle W_{\text{AB}}=\int _{\text{A}}^{\text{B}}\mathbf {F} \cdot \mathrm {d} \mathbf {r} \,}$

Esto es, el trabajo viene dado por la integral curvilínea de ${\displaystyle \mathbf {F} }$ a lo largo de la curva ${\displaystyle C}$ que une los dos puntos; en otras palabras, por la circulación de ${\displaystyle \mathbf {F} }$ sobre la curva ${\displaystyle C}$ entre los puntos A y B. Así pues, el trabajo es una magnitud física escalar que dependerá en general de la trayectoria que una los puntos A y B, a no ser que la fuerza ${\displaystyle \mathbf {F} }$ sea conservativa, en cuyo caso el trabajo resultará ser independiente del camino seguido para ir del punto A al punto B, siendo nulo en una trayectoria cerrada. Así, podemos afirmar que el trabajo no es una variable de estado.